Лаборатория физики высоких энергий
Заведующий лабораторией
Аушев Тагир Адул-Хамидович
д.ф.-м.н., проф., ч.-к., Российская академия наук
Публикаций
1 444
Цитирований
47 664
Индекс Хирша
95
Необходимо авторизоваться.
Лаборатория создана в 2014 году по конкурсу, проводимому в рамках Программы 5-100 МФТИ, и работает в области физики высоких энергий и элементарных частиц, участвует в эксперименте CMS в научно-исследовательском центре CERN, Швейцария, в исследованиях коллабораций MPD и BM@N ускорителе NICA, Россия. Исследования в области блокчейна. Направления деятельности: - изучение распадов В-мезонов в эксперименте CMS в CERN; - разработка методов и изучение фундаментальных свойств квантовых полей на гравитационном фоне - М-теория и супергравитация - применение статистических методов анализа данных в смежных областях науки и технологии, создание моделей для «больших данных» (big-data processing) и т.д. - исследования в области Distributed Ledger Technology, использующие блокчейн-технологии, - участие в исследованиях международных коллабораций MPD и BM@N на строящемся ускорителе NICA (Россия). Лаборатория в рамках своей работы взаимодействует с следующими российскими и зарубежными организациями CERN, Швейцария, ОИЯИ, Дубна, Россия, ИТЭФ, Москва, Россия, IBM, ГМК «Норильский Никель», АО «Основа»
- Экспериментальные методы исследования
- Физические модели
- Техника Келдыша
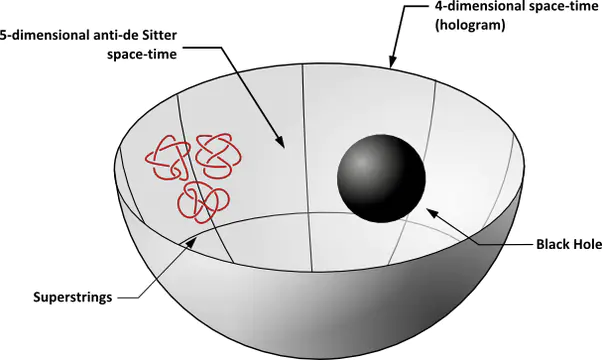
- Голографческое соответствие
- Непертурбативные симметрии в теории струн
Тагир Аушев
Заведующий лабораторией
Эмиль Ахмедов
Ведущий научный сотрудник
Кирилл Губарев
Младший научный сотрудник
Ангелина Бочкова
Стажёр-исследователь
Всего публикаций
1324
Всего цитирований
47472
Цитирований на публикацию
35.85
Среднее число публикаций в год
55.17
Годы публикаций
2001-2024 (24 года)
h-index
95
i10-index
944
m-index
3.96
o-index
401
g-index
158
w-index
23
Описание метрик
h-index
Учёный имеет индекс h, если h из его N статей цитируются как минимум h раз каждая, в то время как оставшиеся (N - h) статей цитируются не более чем h раз каждая.
i10-index
Число статей автора, получивших не менее 10 ссылок каждая.
m-index
m-индекс ученого численно равен отношению его h-индекса к количеству лет, прошедших с момента первой публикации.
o-index
Среднее геометрическое h-индекса и числа цитирований наиболее цитируемой статьи ученого.
g-index
Для данного множества статей, отсортированного в порядке убывания количества цитирований, которые получили эти статьи, g-индекс это наибольшее число, такое что g самых цитируемых статей получили (суммарно) не менее g2 цитирований.
w-index
Если w статей ученого имеют не менее 10w цитирований каждая и другие статьи меньше, чем 10(w+1) цитирований, то w-индекс исследователя равен w.
Топ-100
Области наук
|
100
200
300
400
500
600
700
|
|
|
Nuclear and High Energy Physics
|
Nuclear and High Energy Physics, 616, 46.53%
Nuclear and High Energy Physics
616 публикаций, 46.53%
|
|
General Physics and Astronomy
|
General Physics and Astronomy, 301, 22.73%
General Physics and Astronomy
301 публикация, 22.73%
|
|
Physics and Astronomy (miscellaneous)
|
Physics and Astronomy (miscellaneous), 105, 7.93%
Physics and Astronomy (miscellaneous)
105 публикаций, 7.93%
|
|
Engineering (miscellaneous)
|
Engineering (miscellaneous), 105, 7.93%
Engineering (miscellaneous)
105 публикаций, 7.93%
|
|
Instrumentation
|
Instrumentation, 25, 1.89%
Instrumentation
25 публикаций, 1.89%
|
|
Mathematical Physics
|
Mathematical Physics, 22, 1.66%
Mathematical Physics
22 публикации, 1.66%
|
|
Multidisciplinary
|
Multidisciplinary, 4, 0.3%
Multidisciplinary
4 публикации, 0.3%
|
|
Atomic and Molecular Physics, and Optics
|
Atomic and Molecular Physics, and Optics, 3, 0.23%
Atomic and Molecular Physics, and Optics
3 публикации, 0.23%
|
|
Astronomy and Astrophysics
|
Astronomy and Astrophysics, 2, 0.15%
Astronomy and Astrophysics
2 публикации, 0.15%
|
|
Spectroscopy
|
Spectroscopy, 1, 0.08%
Spectroscopy
1 публикация, 0.08%
|
|
Structural Biology
|
Structural Biology, 1, 0.08%
Structural Biology
1 публикация, 0.08%
|
|
Computer Science (miscellaneous)
|
Computer Science (miscellaneous), 1, 0.08%
Computer Science (miscellaneous)
1 публикация, 0.08%
|
|
Software
|
Software, 1, 0.08%
Software
1 публикация, 0.08%
|
|
100
200
300
400
500
600
700
|
Журналы
|
50
100
150
200
250
300
350
400
450
|
|
|
Physical Review D
418 публикаций, 31.57%
|
|
|
Physical Review Letters
296 публикаций, 22.36%
|
|
|
Journal of High Energy Physics
271 публикация, 20.47%
|
|
|
Physics Letters, Section B: Nuclear, Elementary Particle and High-Energy Physics
162 публикации, 12.24%
|
|
|
European Physical Journal C
109 публикаций, 8.23%
|
|
|
Journal of Instrumentation
24 публикации, 1.81%
|
|
|
Physical Review C
11 публикаций, 0.83%
|
|
|
Progress of Theoretical and Experimental Physics
6 публикаций, 0.45%
|
|
|
Nature Physics
5 публикаций, 0.38%
|
|
|
Nature
3 публикации, 0.23%
|
|
|
Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment
3 публикации, 0.23%
|
|
|
Nuclear Physics A
3 публикации, 0.23%
|
|
|
Computing and Software for Big Science
2 публикации, 0.15%
|
|
|
Reports on Progress in Physics
1 публикация, 0.08%
|
|
|
European Physical Journal A
1 публикация, 0.08%
|
|
|
Journal of the American Society for Mass Spectrometry
1 публикация, 0.08%
|
|
|
Chinese Physics C
1 публикация, 0.08%
|
|
|
Science Bulletin
1 публикация, 0.08%
|
|
|
International Journal of Modern Physics A
1 публикация, 0.08%
|
|
|
AIP Conference Proceedings
1 публикация, 0.08%
|
|
|
Physics of Atomic Nuclei
1 публикация, 0.08%
|
|
|
Journal of the Physical Society of Japan
1 публикация, 0.08%
|
|
|
Nuclear Physics B - Proceedings Supplements
1 публикация, 0.08%
|
|
|
Proceedings of the 15th Lomonosov Conference on Elementary Particle Physics: Particle Physics at the Tercentenary of Mikhail Lomonosov
1 публикация, 0.08%
|
|
|
50
100
150
200
250
300
350
400
450
|
Цитирующие журналы
Издатели
|
100
200
300
400
500
600
700
800
|
|
|
American Physical Society (APS)
725 публикаций, 54.76%
|
|
|
Springer Nature
391 публикация, 29.53%
|
|
|
Elsevier
170 публикаций, 12.84%
|
|
|
IOP Publishing
26 публикаций, 1.96%
|
|
|
Oxford University Press
6 публикаций, 0.45%
|
|
|
World Scientific
2 публикации, 0.15%
|
|
|
American Chemical Society (ACS)
1 публикация, 0.08%
|
|
|
Pleiades Publishing
1 публикация, 0.08%
|
|
|
AIP Publishing
1 публикация, 0.08%
|
|
|
Physical Society of Japan
1 публикация, 0.08%
|
|
|
100
200
300
400
500
600
700
800
|
Организации из публикаций
Страны из публикаций
Цитирующие организации
|
500
1000
1500
2000
2500
3000
3500
4000
|
|
|
Организация не определена
|
Организация не определена, 3873, 8.16%
Организация не определена
3873 цитирования, 8.16%
|
|
Национальный институт ядерной физики
1421 цитирование, 2.99%
|
|
|
Европейская организация по ядерным исследованиям
1074 цитирования, 2.26%
|
|
|
Институт физики высоких энергий Китайской академии наук
869 цитирований, 1.83%
|
|
|
Пекинский университет
784 цитирования, 1.65%
|
|
|
Университет Китайской академии наук
763 цитирования, 1.61%
|
|
|
Университет Париж-Сакле
723 цитирования, 1.52%
|
|
|
Национальный институт ядерной физики и физики элементарных частиц
681 цитирование, 1.43%
|
|
|
Университет Валенсии
591 цитирование, 1.24%
|
|
|
Немецкий Электронный Синхротрон
588 цитирований, 1.24%
|
|
|
Национальная лаборатория Фраскати
561 цитирование, 1.18%
|
|
|
Университет Цинхуа
532 цитирования, 1.12%
|
|
|
Римский Университет Ла Сапиенца
514 цитирований, 1.08%
|
|
|
Институт корпускулярной физики
505 цитирований, 1.06%
|
|
|
Объединённый институт ядерных исследований
504 цитирования, 1.06%
|
|
|
Университет науки и технологий Китая
483 цитирования, 1.02%
|
|
|
Цюрихский университет
474 цитирования, 1%
|
|
|
Рейнский Боннский университет Фридриха Вильгельма
474 цитирования, 1%
|
|
|
Ланьчжоуский университет
454 цитирования, 0.96%
|
|
|
Университет штата Огайо
451 цитирование, 0.95%
|
|
|
Майнцский университет имени Иоганна Гутенберга
449 цитирований, 0.95%
|
|
|
Национальная лаборатория имени Лоуренса в Беркли
448 цитирований, 0.94%
|
|
|
Брукхейвенская национальная лаборатория
444 цитирования, 0.94%
|
|
|
Бэйханский университет
433 цитирования, 0.91%
|
|
|
Массачусетский технологический институт
428 цитирований, 0.9%
|
|
|
Национальный центр ядерных исследований
419 цитирований, 0.88%
|
|
|
Национальная ускорительная лаборатория Ферми
417 цитирований, 0.88%
|
|
|
Оксфордский университет
411 цитирований, 0.87%
|
|
|
Автономный университет Мадрида
411 цитирований, 0.87%
|
|
|
AGH Научно-технический университет
402 цитирования, 0.85%
|
|
|
Технологический институт Карлсруэ
401 цитирование, 0.84%
|
|
|
Институт современной физики Китайской академии наук
401 цитирование, 0.84%
|
|
|
Институт ядерной физики Польской академии наук
396 цитирований, 0.83%
|
|
|
Нанкинский педагогический университет
392 цитирования, 0.83%
|
|
|
Болонский университет
392 цитирования, 0.83%
|
|
|
Университет Генуи
390 цитирований, 0.82%
|
|
|
Гейдельбергский университет имени Рупрехта и Карла
382 цитирования, 0.8%
|
|
|
Центрально-Китайский педагогический университет
382 цитирования, 0.8%
|
|
|
Манчестерский университет
377 цитирований, 0.79%
|
|
|
Пизанский университет
376 цитирований, 0.79%
|
|
|
Университет Павии
376 цитирований, 0.79%
|
|
|
Научно-исследовательская организация по ускорителям высоких энергий
376 цитирований, 0.79%
|
|
|
Институт теоретической и экспериментальной физики имени А. И. Алиханова
375 цитирований, 0.79%
|
|
|
Национальный университет Тайваня
373 цитирования, 0.79%
|
|
|
Шаньдунский университет
372 цитирования, 0.78%
|
|
|
Туринский университет
370 цитирований, 0.78%
|
|
|
Гамбургский университет
363 цитирования, 0.76%
|
|
|
Университет Висконсин в Мадисоне
363 цитирования, 0.76%
|
|
|
Университет Индианы в Блумингтоне
359 цитирований, 0.76%
|
|
|
Неаполитанский университет имени Фридриха II
356 цитирований, 0.75%
|
|
|
Национальный институт субатомной физики
351 цитирование, 0.74%
|
|
|
Карлов университет
349 цитирований, 0.74%
|
|
|
Афинский национальный университет имени Каподистрии
338 цитирований, 0.71%
|
|
|
Рейнско-Вестфальский технический университет Ахена
338 цитирований, 0.71%
|
|
|
Университет Сан-Паулу
335 цитирований, 0.71%
|
|
|
Уппсальский университет
333 цитирования, 0.7%
|
|
|
Университет имени Сунь Ятсена
330 цитирований, 0.7%
|
|
|
Университет Глазго
327 цитирований, 0.69%
|
|
|
Лаборатория Резерфорда — Эплтона
326 цитирований, 0.69%
|
|
|
Бристольский университет
325 цитирований, 0.68%
|
|
|
Токийский университет
323 цитирования, 0.68%
|
|
|
Имперский колледж Лондона
319 цитирований, 0.67%
|
|
|
Фуданьский университет
318 цитирований, 0.67%
|
|
|
Бостонский университет
317 цитирований, 0.67%
|
|
|
Белградский университет
315 цитирований, 0.66%
|
|
|
Ливерпульский университет
314 цитирований, 0.66%
|
|
|
Мэрилендский университет, Колледж-Парк
314 цитирований, 0.66%
|
|
|
Университет Сорбонна
313 цитирований, 0.66%
|
|
|
Университет Айовы
312 цитирований, 0.66%
|
|
|
Московский государственный университет имени М.В. Ломоносова
311 цитирований, 0.66%
|
|
|
Осакский университет
307 цитирований, 0.65%
|
|
|
Институт теоретической физики Китайской академии наук
306 цитирований, 0.64%
|
|
|
Технический университет Дортмунда
305 цитирований, 0.64%
|
|
|
Кембриджский университет
304 цитирования, 0.64%
|
|
|
Босфорский университет
299 цитирований, 0.63%
|
|
|
Ягеллонский университет
299 цитирований, 0.63%
|
|
|
Университет штата Рио-де-Жанейро
299 цитирований, 0.63%
|
|
|
Миланский университет Бикокка
298 цитирований, 0.63%
|
|
|
Афинский политехнический университет
296 цитирований, 0.62%
|
|
|
Университет Клермон-Овернь
294 цитирования, 0.62%
|
|
|
Чикагский университет
293 цитирования, 0.62%
|
|
Центр исследований и перспективных исследований Национального политехнического института
291 цитирование, 0.61%
|
|
|
Национальная ускорительная лаборатория SLAC
289 цитирований, 0.61%
|
|
|
Университет Карнеги — Меллона
288 цитирований, 0.61%
|
|
|
Институт ядерной физики им. Г.И. Будкера СО РАН
287 цитирований, 0.6%
|
|
|
Падуанский университет
287 цитирований, 0.6%
|
|
|
Аргоннская национальная лаборатория
285 цитирований, 0.6%
|
|
|
Национальный институт физики и ядерной инженерии имени Хории Хулубея
285 цитирований, 0.6%
|
|
|
Университет Уэйна
284 цитирования, 0.6%
|
|
|
Национальный институт Хоми Бхабха
283 цитирования, 0.6%
|
|
|
Институт физики Общества Макса Планка
283 цитирования, 0.6%
|
|
|
Бирмингемский университет
281 цитирование, 0.59%
|
|
|
Эдинбургский университет
279 цитирований, 0.59%
|
|
|
Университет Савойя-Монблан
275 цитирований, 0.58%
|
|
|
Уорикский университет
272 цитирования, 0.57%
|
|
|
Институт физики Хельсинки
272 цитирования, 0.57%
|
|
|
Университет Перуджи
272 цитирования, 0.57%
|
|
|
Университет Тарапаки
272 цитирования, 0.57%
|
|
|
Институт фундаментальных исследований Тата
270 цитирований, 0.57%
|
|
|
Калифорнийский университет в Беркли
268 цитирований, 0.56%
|
|
|
500
1000
1500
2000
2500
3000
3500
4000
|
|
Цитирующие страны
- Мы не учитываем публикации, у которых нет DOI.
- Статистика пересчитывается раз в сутки.
Направления исследований
Поиск тяжелого стерильного нейтрино в распаде Ds- мезона в эксперименте CMS
+
Стандартная модель физики элементарных частиц представляет собой красивую и завершенную теорию, последним кирпичиком которой стало триумфальное открытие бозона Хиггса на Большом адронном коллайдере в ЦЕРНе в 2012 году. Тем не менее, в настоящий момент достаточно очевидно, что она не является теорией всего. Так, например, согласно Стандартной модели, существует три поколения безмассовых нейтральных лептонов: электронное, мюонное и тау-нейтрино. Однако в XXI веке было обнаружено существование нейтринных осцилляций (Нобелевская премия по физике 2015), когда нейтрино одного поколения переходит в другое, что противоречит гипотезе о безмассовости нейтрино (и, следовательно, выходит за рамки Стандартной модели). Другие популярные проблемы Стандартной модели – наличие во Вселенной барионной асимметрии и темную материи – тоже могут быть связаны с наличием ненулевой массы у нейтральных лептонов, именно поэтому в современном мировом сообществе является очень актуальным вопрос поиска Новой Физики – эффектов за пределами Стандартной модели – в области нейтринной физики. Три упомянутые выше проблемы, не объясняемые Стандартной моделью, могут быть решены введением нового типа нейтрино – тяжелого стерильного нейтрино, которое не взаимодействуют с обычным веществом, но обладают большой массой и могут осциллировать в обычные нейтрино Стандартной модели.
Прецизионные измерения параметров тяжелых адронов и поиск Новой Физики в эксперименте CMS
+
За последние пятьдесят лет была теоретически разработана и экспериментально подтверждена современная теория фундаментальных частиц — Стандартная Модель (СМ), последним кирпичиком которой стало триумфальное открытие бозона Хиггса на Большом адронном коллайдере в ЦЕРНе в 2012 году. Несмотря на ее красоту и точность в описании процессов на коллайдерах, существуют ряд космологических наблюдений, требующих расширения СМ (т.е. создание моделей, не противоречащих ей, но выходящих за ее рамки). Частицы, процессы или модели, выходящие за рамки СМ, часто называют Новой Физикой, и ее поиск является наиболее актуальной задачей современной физики элементарных частиц. К сожалению, в области так называемой "high-pt" физики – поиск темной материи, суперсимметричных частиц, экзотических резонансов, нейтральных лептонов – "большие эксперименты" ATLAS и CMS на БАК за 10 лет с открытия бозона Хиггса не добились какого-то существенного прогресса в нахождении отклонений от СМ.
Свойства корреляционных функций в квантовой теории поля, аналитичность, изометрия и нестационарность
+
Мы исследуем свойства корреляционных функций в квантовой теории поля в сильных внешних полях различной природы, а также динамику начального состояния в нестационарных ситуациях. При рассмотрении таких симметрических пространств, как пространства Минковского, де Ситтера и анти де Ситтера, и инвариантных относительно соответствующих изометрий состояний, важно изучение аналитических свойств корреляторов и петлевых поправок к ним, как функций геодезических расстояний. В случае же более общих, не инвариантных, состояний и фоновых полей важно изучение динамики начального состояния. А именно исследование нестационарных явлений, когда, например, фон зависит от времени, требует включение в рассмотрение состояний с ненулевыми аномальными средними и заселенностями уровней, так как эти величины генерируются динамически в петлях во многих моделях со взаимодействием во внешних полях, и в присутствии двигающихся зеркал. Также с прикладной точки зрения самой актуальной проблемой является динамика фермионов в моделях с взаимодействием и в сильном магнитном поле при высокой плотности или при низких температурах. Помимо всего прочего, исследование динамики в этих системах может пролить свет на физику динамического образования конденсата и ответить на вопрос о существовании островков стабильности в плазме высокой плотности.
Теоретико-полевые методы в М-теории
+
С момента открытия АдС/КТП соответствия во второй половине 90-х годов теория струн вместе с ее непертурбативной формулировкой, М-теорией, вызывают большой интерес как мощные инструменты исследования калибровочных теорий. Точкой приложения оказываются не только феноменологически интересные теория, такие как суперсимметричная КХД или теории, описывающие сильно-кореллированные системы, но и модели, связанные с более фундаментальными вопросами, такими как определение и подсчет микроскопических степеней свободы черных дыр. В данной контексте особенно полезными оказываются методы генерации решений, позволяющие исследовать свойства семейств калибровочных теорий поля, генерировать новые калибровочные теории и получать информацию о нелагранжевых операторах, используя геометрические свойства решений супергравитации, являющейся низкоэнергетическим пределом теории струн и М-теории. Известным примером является бивекторная янг-бакстерова деформация фона AdS5xS5, дуальная т.н. бета-деформации Ли-Штрасслера теории N=4 супер Янга-Миллса, сохраняющая N=1 суперсимметрию. Настоящий проект посвящен развитию и приложению к конкретным решениям методов генерации решений, предложенных в рамках выполнения проекта 2020. Развиваемые методы основаны на U-ковариантном формализме исключительной теории поля, которая описывает низкоэнергетическую динамику М-теории и, вообще говоря, выходит за рамки стандартной 11-мерной супергравитации. Ожидается, что, успешно пройдя апробацию на наиболее простых примерах, эти методы станут эффективным инструментом для контролируемой генерации новых несуперсимметричных семейств конформных теорий поля, исследования соответствующей динамики мембран и расширения пространства самосогласованных вакуумов М-теории.
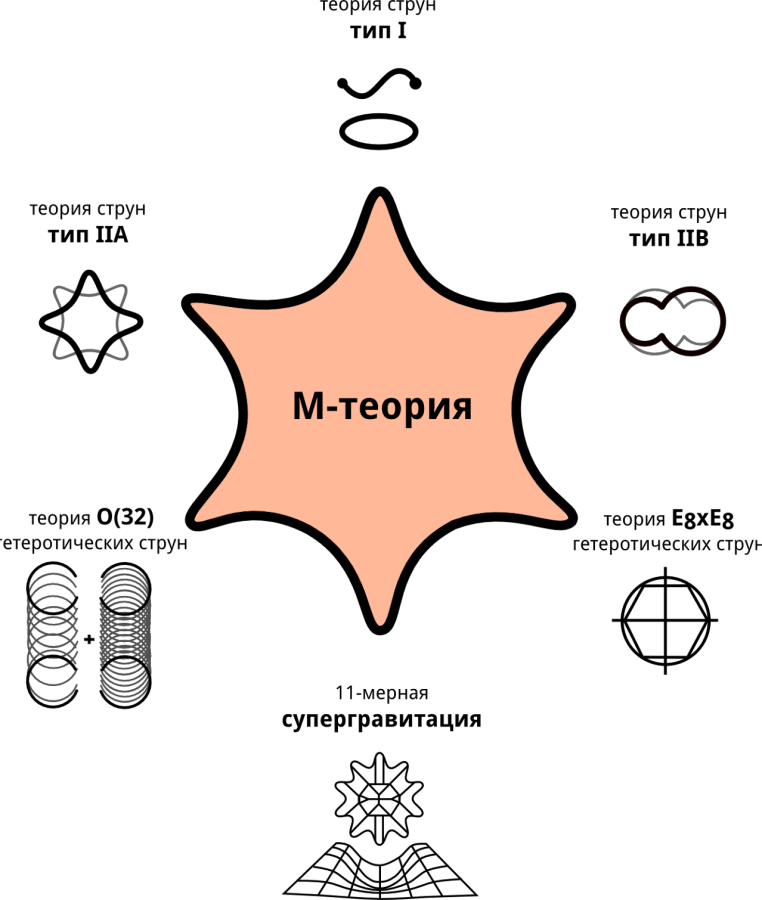
Динамика экзотических бран и негеометрические компактификации
+
Проект направлен на изучение динамики экзотических бран, которые, несмотря на название, являются такими же фундаментальными объектами в теории струн, как, например, D-браны и сама струна. Предлагается изучение этих объектов, как с фундаментальной точки зрения, так и в теоретико-полевом пределе. В первом случае в фокусе оказывается эффективное действие для экзотических бран, во втором — геометрические свойства соответствующих конфигураций пространства и полей. Основным инструментом в рамках проекта предполагается т.н. двойная (исключительная) теория поля, в формализме которой симметрия относительно Т(U)-дуальности оказывается явной, что позволяет развить единый подход к экзотическим и обычным бранам. Экзотические браны являются партнерами стандартных D- и NS-бран под действием преобразований Т-дуальности. На уровне супергравитации они проявляются в виде особых решений, которые глобально определены только с точностью до преобразования Т(U)-дуальности, и в самых простых случаях соответствуют T(U)-образиям. Кроме этого, известно, что экзотические браны взаимодействуют со специального рода потенциалами, потоки которых позволяют получать вакуумы с малой положительной космологической постоянной. Т.н. негеометрические компактификации
Методы генерации решений супергравитации и АдС/КТП соответствие
+
Дуальность калибровочной гравитации и, в частности, соответствие AdS/CFT, являются, вероятно, наиболее успешным применением методов теории струн для анализа калибровочных теорий. Эти дуальности вызывают большой интерес в контексте феноменологических приложений к многочастичным системам, таким как сверхпроводимость, нефермиевские жидкости, энтропия запутанности и многие другие. Богатая симметрия пространства вакуумов теорий струн позволяет выйти далеко за рамки стандартной слабой/сильной связи. соответствие и описывать теории с меньшим количеством симметрий, чем N = 4 SYM. Среди таких симметрий наиболее важными для предлагаемого проекта являются преобразования, генерирующие решения, основанные на неабелевых Т-дуальности, деформации Янга-Бакстера десятимерных фонов супергравитации и в более общем смысле Т-двойственности Пуассона-Ли. Этот проект направлен на продвижение методов генерации решений, разработанных для струнных сигма-моделей и 10-мерной супергравитации, до уровня 11-мерной супергравитации. Десятимерный фон супергравитации описывает очень ограниченные локусы в пространстве модулей вакуума теории струн, где константа связи струн мала и пертурбативное описание допустимо. Однако в целом наблюдается 11-е направление, а постоянные струнные вакуумы соответствуют фону 11-мерной супергравитации. В некоторой степени можно продвигать двойственность калибровочной гравитации в 11-мерную теорию и калибровочные теории, описывающие системы бран М-теории. Недавно в литературе было предложено 11-мерное обобщение деформаций Янга-Бакстера фона супергравитации, однако, несмотря на очень мало игрушечных примеров, о таких деформациях доступно не так много информации. В частности, известно, что они имеют отношение к процедуре неабелевых преобразований U-дуальности, предложенной недавно в литературе. Следовательно, естественно интересуются теми же вопросами, что и в 10-мерном случае: сохранение интегрируемости, явные деформации 11-мерного фона, генерация новых теорий поля с помощью неабелевой U-двойственности, анализ спектра оп- сторонники деформированных теорий и т. д. Основными целями проекта являются: разработка инструментов генерации решений для основы М-теории, анализ свойств двойственных суперконформных теорий поля, включая РГ-поведение, некоммутативность и операторный спектр, поиск классификаций, регулирующих алгебраическую основу методов. Что касается калибровочной теории, мы ожидаем получить новые результаты и/или новые интерпретации известных результатов на основе разработанных инструментов. Что касается сигма-модели, мы ожидаем получить представление о недавно предложенных деформациях 11-мерных фонов и получить доступ к их свойствам интегрируемости. Проблемы будут решаться с использованием новых методов, разработанных как приложения исключительного подхода теории поля: неабелева и U-двойственность Намбу-Ли, исключительная алгебра Дринфельда, исключительная спектроскопия Калуцы-Клейна, поливекторные деформации.
Публикации и патенты
Найдено
Ничего не найдено, попробуйте изменить настройки фильтра.
Партнёры
АО «Основа»
Адрес лаборатории
Институтский переулок, 9с2
Необходимо авторизоваться.